

Next: 规则网络与随机网络
Up: 从统计物理学看复杂网络研究
Previous: 加权网络
上一节我们主要总结了对于实际网络的静态性质的统计研究,这一节我们去看一看什么样的网络模型会展现这些特定的统计性质。这是
研究网络上的动力学模型的基础。如考虑不同网络上的传染病模型,用来描述接触性传染病的传播,谣言在人群中的传播等现象,或者
不同网络上的渗流模型。对于这些问题,我们可以选择用微分方程来描述。例如以下Logistic模型,
我们把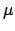 看成是健康人与受感染人之间发生接触并获得传染的几率。所以在此模型中,所有个体是均匀混合的,没有局域近邻的概念,就
好像是溶液中发生的化学反应一样。或者我们这样来理解
看成是健康人与受感染人之间发生接触并获得传染的几率。所以在此模型中,所有个体是均匀混合的,没有局域近邻的概念,就
好像是溶液中发生的化学反应一样。或者我们这样来理解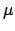 ,把疾病看作只要接触就传染,那么
,把疾病看作只要接触就传染,那么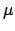 的意义是平均来看每一个体的近邻数
目占所有人口的比例。由此可见,Logistic模型的背景是完全随机网络。作为补充,我们可以在规则网络上用模拟或者重整化群的方法来研究
这一问题。而作为模型真实背景的是人的社会交往的网络。这样一些网络可以通过实证研究获得对其静态性质一定的认识。但是对于研究这些
网络上的动力学模型来说,更加广泛的研究还需要网络模型,而不仅仅是实际网络数据。例如,人类相互认识的网络是Small World网络,那么
当我们研究这样的网络上的动力学模型的时候,我们就需要一个相应特征的网络来作为我们的背景。当然,我们可以收集这个网络的实际信息,
然后在这个实际网络上进行分析。但是这有很大的局限性,尤其对于理论研究。如果我们能够设计一个具有这些性质的网络演化机制模型,那
么我们进一步对网络上动力学模型的研究就可以以这些机制模型为基础。从另外一个角度来说,既然网络的静态几何性质研究给出来实际网络
中存在的一些普适性质,那么从理论上构造机制模型来解释这些网络的形成与发展,也是一个重要的物理问题。本节中,我们将分别介绍规则
网络和完全随机网络[5](以下简称随机网络),Small World网络[7]与Scale Free网络[18]的机制模型。
的意义是平均来看每一个体的近邻数
目占所有人口的比例。由此可见,Logistic模型的背景是完全随机网络。作为补充,我们可以在规则网络上用模拟或者重整化群的方法来研究
这一问题。而作为模型真实背景的是人的社会交往的网络。这样一些网络可以通过实证研究获得对其静态性质一定的认识。但是对于研究这些
网络上的动力学模型来说,更加广泛的研究还需要网络模型,而不仅仅是实际网络数据。例如,人类相互认识的网络是Small World网络,那么
当我们研究这样的网络上的动力学模型的时候,我们就需要一个相应特征的网络来作为我们的背景。当然,我们可以收集这个网络的实际信息,
然后在这个实际网络上进行分析。但是这有很大的局限性,尤其对于理论研究。如果我们能够设计一个具有这些性质的网络演化机制模型,那
么我们进一步对网络上动力学模型的研究就可以以这些机制模型为基础。从另外一个角度来说,既然网络的静态几何性质研究给出来实际网络
中存在的一些普适性质,那么从理论上构造机制模型来解释这些网络的形成与发展,也是一个重要的物理问题。本节中,我们将分别介绍规则
网络和完全随机网络[5](以下简称随机网络),Small World网络[7]与Scale Free网络[18]的机制模型。
Subsections
wwwwjs
2004-01-04