规则网络与随机网络

我们把一维链，二维正方晶格等称为规则网络。规则网络是指平移对称性晶格，任何一个格点的近邻数目都相同。当然这只是一个习惯用法， 不是下定义，比如Carley Tree显然不是随机网络，但是也没有规定说它属于规则网络。随机网络是另一个极端，由N个顶点构成的图中， 可以存在C²_N条边，我们从中随机连接M条边所构成的网络就叫随机网络。还有一种生成随机网络的方法是，给一个概率p， 对于C²_N中任何一个可能连接，我们都尝试一遍以概率p的连接。如果我们选择 M = pC²_N，这两种随机网络模型就可以联系 起来。对于如此简单的随机网络模型，其几何性质的研究却不是同样的简单。随机网络几何性质的研究是由Paul Erdös，Alfréd Rényi 和Béla Bollobás在五十年代到六十年代之间完成的。为了强调随机网络研究与统计物理学的联系，我们从系综理论的角度重新表述 了随机网络统计性质的研究结果。但是，为了在这一节中突出模型的统计性质而不是处理方法，我们把这一表述放在最后专门介绍方法与技术 的一节中。

规则网络与随机网络的典型几何性质包括：度分布，平均集聚程度与平均最短距离。规则网络所有顶点都相同，因此其度值相同，度分布 为 $\delta$$\left(\vphantom{k-k_{0}}\right.$k - k₀$\left.\vphantom{k-k_{0}}\right)$，其平均集聚程度也只需要在一个点计算 C = $\left<\vphantom{C_{v}}\right.$C_v$\left.\vphantom{C_{v}}\right>$ = C_v， 其最短距离可以也只从某一个顶点开始计算从它到所有其他顶点之间的距离之和 L $\sim$ N²，然后计算其平均值 d = ${\frac{{L\times N}}{{2\times C^{2}_{N}}}}$ $\sim$ N。对于随机网络 G$\left(\vphantom{N,p}\right.$N, p$\left.\vphantom{N,p}\right)$，包含了从空图到完全图的所有可能情况，因此随 机图的几何性质需要对每一种可能图做平均，例如我们计算每一种可能图的最短距离，然后按照各自出现的几率做平均。 一般公式与详细的计算见第7节。研究结果表明随机网络顶点的度值符合平均值为pN的泊松分布， 其集聚程度约等于p，最短距离 d $\sim$ ln(N)。

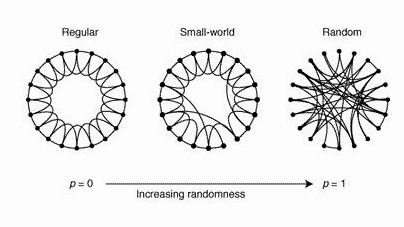
对比规则网络与随机网络，我们发现，平均集聚程度与平均最短距离，这两个静态几何量能够很好地反映规则网络与随机网络的性质及其差异。 规则网络的特征是平均集聚程度高而平均最短距离长，随机网络的特征是平均集聚程度低而平均最短距离小。 规则网络的平均最短距离d $\sim$ N，而其集聚程度依赖于近邻数目k₀，例如在如图(1)所示的规 则网络中，k₀ = 4，集聚程度为 ${\frac{{1}}{{2}}}$。而在随机网络中，平均集聚程度非常的小，在图(1) 所示的随机网络中，顶点数与边数都与规则网络相同，但集聚程度为0.02。

Fig 1: Small World网络模型，图中所示的Small World网络是在左图的规则网络基础上通过边的重连得到的。p为每一条边的重连几率。当p = 0时，成为规则网络，p = 1.0时成为随机网络。本图取自文献[7]。

然而正是由于其集聚程度非常地小，所以其平均最短距离小。考察一个顶点u的近邻，假设其近邻数为a，那么在 a个近邻的近邻之中相互重复的个数非常少，所以从u出发经过两次近邻关系我们可以找到正比于a²的新顶点，最多经过log_aN 个近邻关系，我们就可以穷尽整个网络。所以，其最短距离满足 d $\sim$ ln N。可见，对于规则网络，也正是由于其集聚程度高，重复率很 大，所以平均最短距离大。如此看来好像这是一对相互矛盾的几何量。

那么，是否存在一个同时具有高集聚程度，小最短路径的网络呢？对于传染病模型，平均集聚程度对应于传播的广度，平均最短距离代表的 是传播的深度。因此，如果实际网络同时存在宽的广度和大的深度的话，在这样的网络上的传染病传播显然将大大高于规则网络与随机网 络。Watt和Strogatz为我们找到了这样的网络模型--Small World网络[3,7]。