在Small World网络的研究兴起之后,越来越多的科学家投入到复杂网络的研究中去。大家发现其实更多的其他几何量的特征也具有很大程 度上的普适性和特定的结构功能关系。Scale Free网络就是其中的一个重要方面。Scale Free网络指的是网络的度分布符合幂率分布,由于 其缺乏一个描述问题的特征尺度而被称为无标度网络。我们都知道在统计物理学相变与临界现象,以及在自组织临界性(SOC)中幂率具有 特殊地位[25]。这种度分布的无标度性是否也会带来网络上动力学模型的特殊性质呢?我们也将在下一节网络的动力学性质加以总结。实证研究 发现,大量的实际网络可以被认为是Scale Free网络[1],见表2。
4表2:实际网络的Scale Free现象。列表中包括所研究网络的实际对象(Network),大小(Size),
平均度值(< k >),Out度幂率分布指数(
![]() ),In度幂率分布指数(
),In度幂率分布指数(
![]() ),
平均最短距离(l),按随机网络计算的最短距离(lrand)。可见,Scale Free网络一般具有Small World
特征。此表在文献[1]的基础上收集确认其他文献编辑而成,感谢作者R. Albert提供。
),
平均最短距离(l),按随机网络计算的最短距离(lrand)。可见,Scale Free网络一般具有Small World
特征。此表在文献[1]的基础上收集确认其他文献编辑而成,感谢作者R. Albert提供。
| Network | Size |
|
|
|
lreal | lrand |
| WWW[50] | 325, 729 | 4.51 | 2.45 | 2.1 | 11.2 | 8.32 |
| WWW[29] | 43, 107 | 7 | 2.38 | 2.1 | ||
| WWW[27] | 23, 108 | 7.5 | 2.72 | 2.1 | 16 | 8.85 |
| WWW[30], site | 260, 000 | 1.94 | ||||
| Internet[44], domain | 3015 - 4389 | 3.42 - 3.76 | 2.1 - 2.2 | .1 - 2.2 | 4 | 6.3 |
| Internet[44], router | 3888 | 2.57 | 2.48 | 2.48 | 12.15 | .75 |
| Internet[45], router | 150, 000 | 2.66 | 2.4 | 2.4 | 11 | 12.8 |
| Movie actors[18] | 212, 250 | 28.78 | 2.3 | 2.3 | 4.54 | 3.65 |
| Co-authors[66] , SPIRES | 56, 627 | 173 | 1.2 | 1.2 | 4 | 2.12 |
| Co-authors[67] , neuro. | 209, 293 | 11.54 | 2.1 | 2.1 | 6 | .01 |
| Co-authors[67], math. | 70, 975 | 3.9 | 2.5 | 2.5 | 9.5 | 8.2 |
| Sexual contacts[47] | 2, 810 | 3.4 | 3.4 | |||
| Metabolic[51] , E. coli | 778 | 7.4 | 2.2 | 2.2 | 3.2 | 3.32 |
| Protein[48] , S. cerev.* | 1, 870 | 2.39 | 2.4 | 2.4 | ||
| Citation[65] | 783, 339 | 8.57 | 3 | |||
| Phone call[28] | 533, 106 | 3.16 | 2.1 | 2.1 | ||
| Words[49], co-occurrence* | 460, 902 | 70.13 | 2.7 | 2.7 |
现在我们来看看Scale Free网络的形成机制。目前对于无向Scale Free网络,普遍认为偏好依附(Preferential Attachment)[18]是一个很好地
形成Scale Free网络的机制。具体模型如下。取初始m0个顶点任意连接或完全连接。每一步在原网络
G![]() t - 1
t - 1![]() 的基础上加
上一个新的顶点,同时加上从此顶点出发的m条边,形成新的网络
G
的基础上加
上一个新的顶点,同时加上从此顶点出发的m条边,形成新的网络
G![]() t
t![]() 。其中新加边的另一个端点按照正比于顶点度数的分
布
。其中新加边的另一个端点按照正比于顶点度数的分
布
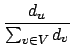
|
(13) |
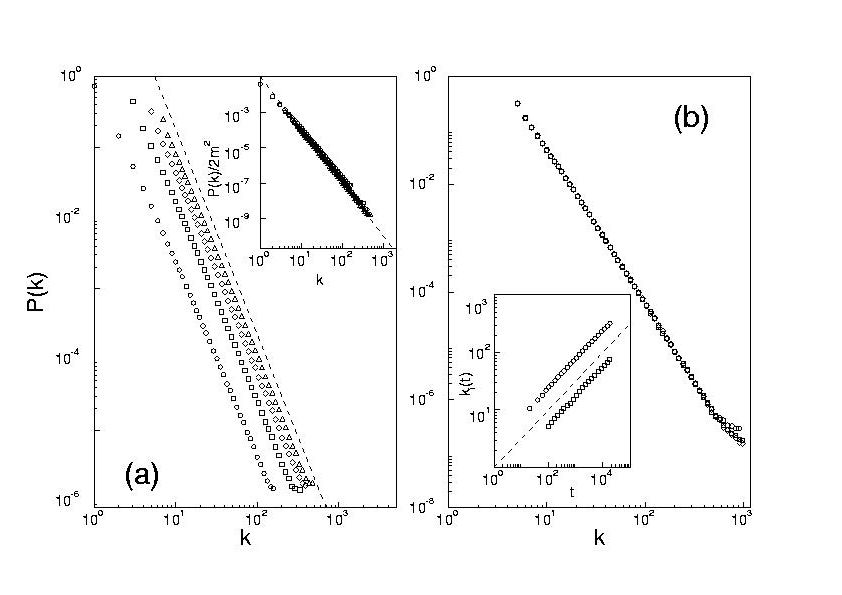
鉴于实际网络的幂指数并不都是![]() = 3,有的作者发展了Barabási和Albert的原始偏好依附模型,使得幂指数可以用模型参
数来调整。在偏好依附模型中,顶点v的度值kv可以认为是其吸引力的度量。那么,随着时间的推移,除去少数精品之外,大多数
的顶点的吸引力会随着时间减弱。一个考虑了顶点历史的模型[23]可以改变幂指数
= 3,有的作者发展了Barabási和Albert的原始偏好依附模型,使得幂指数可以用模型参
数来调整。在偏好依附模型中,顶点v的度值kv可以认为是其吸引力的度量。那么,随着时间的推移,除去少数精品之外,大多数
的顶点的吸引力会随着时间减弱。一个考虑了顶点历史的模型[23]可以改变幂指数![]() 。更多的可调参数模型甚至是破坏幂率分布的模型
可以通过考虑更一般的网络演化过程得到。
。更多的可调参数模型甚至是破坏幂率分布的模型
可以通过考虑更一般的网络演化过程得到。
另外一个要改动偏好依附模型的要求是偏好依附模型并不能复现所有的认为是Scale Free网络的静态特征。对于大多数实际Scale Free 网络所展现的Small World现 象,模型给出了较好的结果,但是模型的度度相关性为零,这与实际网络中存在的匹配模式不相符合[16]。更多的关于其他几 何量的实际与模型的对比,以及在对比基础上对模型的修改工作还有很多值得做的地方。比如Goh 和Oh等给出了模型上的介数的分布 规律[17],但是更广泛的实证分析仍然有待完成。这些相符的或者不相符的现象都给出了模型推广与修改的方向。
作为一个一般的网络演化
的框架有哪些现象是可以进入模型来考虑的呢?一个一般的网络演化包含五种现象:加点、加边、重连、去边、去点。所谓加点就是t时刻
在图
G![]() t - 1
t - 1![]() 上加上新的顶点,并且加上若干从此顶点出发的边;加边指的是t时刻在
G
上加上新的顶点,并且加上若干从此顶点出发的边;加边指的是t时刻在
G![]() t - 1
t - 1![]() 原有顶点之间新
加入若干连接;去边与去点则是以上过程的逆;而先去边后加边合起来就是重连,但是只有当加边和去边发生在同一顶点上的时候才刚好是
重连,所以鉴于重连事件的几率有可能大大大于去边和加边发生几率之乘积,所以把重连独立出来。目前绝大多数网络演化模型都在这五种
事件的范围内讨论。
原有顶点之间新
加入若干连接;去边与去点则是以上过程的逆;而先去边后加边合起来就是重连,但是只有当加边和去边发生在同一顶点上的时候才刚好是
重连,所以鉴于重连事件的几率有可能大大大于去边和加边发生几率之乘积,所以把重连独立出来。目前绝大多数网络演化模型都在这五种
事件的范围内讨论。
在这样一个框架下来看,我们看到偏好依附模型只考虑了加点的行为,只是对于加点以后建立的从新加点出发的连接做了偏好性假定。
从Barabási和Albert提出此模型以后,许多作者讨论了此模型的变例。Dorogovtsev,Mendes和Samukhin的模型[19]讨论了新加点加入之后,
m条新加边可以不从此点出发的模型,维持偏好性不变。模型还区分了In和Out边,并且基于In度提出了吸引力的概念,认为顶点v的吸
引力就是
Av = A + kinv。此模型也能呈现幂率的度分布,并且幂指数可调
![]() = 2 +
= 2 + ![]() 。其实我们可以看到,实际上,
此模型相当于考虑了加点和加边两件事情,只是由新加点引起的边不是一个确定数,内部原有点之间的新加边也不是确定数,但是仍然
都维持偏好性。当我们只考虑In度分布的时候,可以忽略新加边Out端点的选择而只考虑In端点的偏好性。
。其实我们可以看到,实际上,
此模型相当于考虑了加点和加边两件事情,只是由新加点引起的边不是一个确定数,内部原有点之间的新加边也不是确定数,但是仍然
都维持偏好性。当我们只考虑In度分布的时候,可以忽略新加边Out端点的选择而只考虑In端点的偏好性。
有两个试验可以探讨加点和偏好性在模型中的不同地位。第一个试验是只考虑加点,但是从新点出发的边的端点的选择不满足偏好性,而是 随机选取。模型给出了指数衰减的分布[18]。另外一个试验是只考虑加边。从一个非常稀 疏的N顶点M边的随机网络开始,每一步就是随机选一个顶点,然后按照偏好性选择另一个顶点,如果不存在已连接的边,连之。或者是 同时考虑活性偏好与连接偏好,即第一端点的选择和第二端点的选择都按照偏好依附的形式。当然, 随着重复的次数增加,模型将趋向于完全网络,所以这样的模型的稳态显然不是幂率分布的。但是,是否存在着一个演化区间,在此范围内, 网络呈现幂率分布呢?我们知道如果两个端点都随机选择就是随机网络模型,顶点的度符合泊松分布,那么按照偏好方式选择的随机网络模 型呢?如果在一定时间段出现了幂率分布的话,那说明偏好性是其决定性因素,所谓引入新加点只是使得网络取得某种平衡,不至于发展为 完全网络而已。Barabási等人就研究了这样一个模型[21],发现在演化的初期确实存在幂律形式的度值分布,但是随着时间 的演化逐渐过渡到高斯分布。这说明偏好依附是Scale Free网络的核心机制,但是新加点也不可或缺。
Albert和Barabási的第二个关于Scale Free网络的机制模型[32]考虑了加点、加边、重连三种事件。每一时刻这三个操作分别以某一概率
![]() 1 - p - q, p, q
1 - p - q, p, q![]() 发生,任何一种事件发生都遵循偏好性。理论分析与模拟的结果表明幂率分布与指数分布都可以在网络中出现,取决于
p, q的值--q < qmax为幂率形式的度分布,否则为指数形式。当然,这样的结果肯定是不完全的,因为当p
发生,任何一种事件发生都遵循偏好性。理论分析与模拟的结果表明幂率分布与指数分布都可以在网络中出现,取决于
p, q的值--q < qmax为幂率形式的度分布,否则为指数形式。当然,这样的结果肯定是不完全的,因为当p ![]() 0.5的时候,加边
占统治地位,必然使网络趋向于完全图。所以关于p也存在某一个域值。
0.5的时候,加边
占统治地位,必然使网络趋向于完全图。所以关于p也存在某一个域值。
无向网络模型的一个比较全面的探索是由Cooper和Frieze完成的[34],他们考虑了加边和加点两件事情,并且探讨了有无偏好性对模型的影响。
其演化过程如下,在任一时刻t,以![]() 的几率加边发生在图
G
的几率加边发生在图
G![]() t - 1
t - 1![]() 的原顶点之间,以1 -
的原顶点之间,以1 - ![]() 的几率加入新顶点。
如果加入新顶点,则按照某一分布pi产生一个随机数i表示从此顶点出发的边数,然后以
的几率加入新顶点。
如果加入新顶点,则按照某一分布pi产生一个随机数i表示从此顶点出发的边数,然后以![]() 的几率在原顶点中随机选择另一个
端点,以1 -
的几率在原顶点中随机选择另一个
端点,以1 - ![]() 的几率按照偏好性选择另一端点。如果是在原顶点中加边,则按照某一分布qi产生一个随机数i表示新加的边数。
然后,以
的几率按照偏好性选择另一端点。如果是在原顶点中加边,则按照某一分布qi产生一个随机数i表示新加的边数。
然后,以![]() 的几率在原顶点中均匀选择第一端点,以1 -
的几率在原顶点中均匀选择第一端点,以1 - ![]() 的几率按照偏好性选择第一端点,接着以
的几率按照偏好性选择第一端点,接着以![]() 的几率在原顶点
中均匀选择第二端点,以1 -
的几率在原顶点
中均匀选择第二端点,以1 - ![]() 的几率按照偏好性选择第二端点。文章对于各个参数对于模型的影响都做了理论分析,包括分布形式
的显式结果或上下界分析。
的几率按照偏好性选择第二端点。文章对于各个参数对于模型的影响都做了理论分析,包括分布形式
的显式结果或上下界分析。
再用这个框架去看引入顶点年龄历史的模型[23],我们发现可以认为考虑活性与年龄的关系相当于在一定程度上考虑去点或去边的行为。
最后,一个关键性机制突出,又能最大程度上复现相关几何性质,包含一般的网络演化五种现象的机制模型,将是无向Scale Free网络模型的
最终目标。除了以偏好依附为基础的这一大类模型之外,还存在一类特殊的确定性Scale Free网络--等级结构网络,见Barabási等人的
文章[8]。对于实证研究而言,有一个静态统计量能够很好地区分这两类模型--顶点集聚程度的分布规律
p![]() cv
cv![]() 。
。
从有向网络的角度来看,无向网络的偏好依附模型可以认为是只存在In度幂率分布,Out度为
![]()
![]() dout - m
dout - m![]() 分布
或某种平庸随机分布的演化模型。既然实证研究表明了双向幂率网络的普遍性,那么机制模型的研究工作就需要对此做出回答。
对于双向幂率分布模型,如果在单向幂率分布模型的基础上把所有的单向边都换成双向边,那自
然就有了双向幂率分布。所以双向比--双向边占所有边的比例对于有向网络来说是一个重要静态几何量。
分布
或某种平庸随机分布的演化模型。既然实证研究表明了双向幂率网络的普遍性,那么机制模型的研究工作就需要对此做出回答。
对于双向幂率分布模型,如果在单向幂率分布模型的基础上把所有的单向边都换成双向边,那自
然就有了双向幂率分布。所以双向比--双向边占所有边的比例对于有向网络来说是一个重要静态几何量。
还有一种实现双向幂率
模型的方式是独立地构造In和Out边的机制,例如类比于按照偏好性建立的In边的反馈机制,我们也可建立Out边的反馈机制。基于以上想
法,Tadic建立了以下模型[33]。从m0顶点M边的随机网络开始,在t时刻,以![]() 的几率加入一个新的顶点,并带来从此顶
点出发的m条边,以1 -
的几率加入一个新的顶点,并带来从此顶
点出发的m条边,以1 - ![]() 的几率从原有网络的顶点内产生m条边。从新加顶点出发的边的终点按照偏好性选择,即
的几率从原有网络的顶点内产生m条边。从新加顶点出发的边的终点按照偏好性选择,即
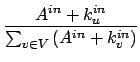
|
(14) |
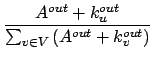 , ,
|
(15) |
还有一个因素也可以在单向幂率的基础上产生双向幂率--In度与Out度的高度相关性。考察每一个顶点的
![]() din, dout
din, dout![]() 之间的相关性,如果存在高度正相关说明,对外联系活跃(Out)的顶点也常常是获得外界联系多(In)的顶点。于是,自然也可以得到双向
幂率分布了。
之间的相关性,如果存在高度正相关说明,对外联系活跃(Out)的顶点也常常是获得外界联系多(In)的顶点。于是,自然也可以得到双向
幂率分布了。
那么真实有向网络的双向幂率结构是否能够由以上这些因素来解释呢?这有待于实证分析来回答,尤其是关于度相关性的实证分析及其与理 论模型的对比在这一点的判定上就有重要价值。如果以上因素都不能够代表实际网络双向幂率结构的形成机制的话,那么研究者就不得不面 对一个包含混合反馈机制的有向网络模型了,比如,In边可以同时受In度和Out度的反馈来影响,Out边也是如此。
最后,我们谈谈加权网络的机制模型。由于加权网络的静态几何量与动力学性质没有得到广泛的研究,所以也就很难对其形成机制进行深入 探讨了。从机制模型的角度来看,加权网络的演化既包含连接的演化又包含权重的演化,而且两者可能相互影响,看来要复杂得多了。