加权网络

首先，我们需要讨论加权网络的加权的必要性与方式。把一个实际问题抽象为加权网络的过程并不都是平庸的。当然，对于邮递员问题等包含距离关系的网络，直接把距离作为权就可以了，但是对于其他包含相似关系、亲密程度等社会关系的网络，如何加权就值得讨论了。尤其是，当系统当中包含多个层次的同一属性的关系的时候，就必须仔细研究其加权方式了。以下，我们以某一学术领域内的科学家网络 [66,68]为例，介绍加权网络。

为了研究某一学术领域的发展变化，某一个新的思想在此领域内的产生、传播，我们构造了一个科学家之间通过文献相互联系影响的网络。我们认为，对于研究此问题而言，科学家之间的合作关系[66]，引文关系[65,68]以及讨论或书信交往（经常体现在致谢中）属于同一属性的关系，但是所起作用的程度有所不同。对于交流思想而言，合作是最直接的影响，其次是引文，再次为致谢。而且，在同为合作的关系内，合作的次数的不同，对于交流思想的影响也是不一样的。因此，在这个科学家网络中，每一条边代表了综合考虑了以上三个方面两个层次的相互作用以后的影响力程度。并且由于引文和致谢的有向性，此网络是一个加权有向网络。

加权网络的静态几何量包括：度及其分布特征，权及其分布特征，权的相关性，权与度的相关性，权与网络结构和效率之间的关系，最短距离及其分布特征，介数及其分布特征与隧道现象，与相应无权网络的对比，距离关系与类聚分析，以及在加权网络上集聚程度的定义及其统计性质。

首先加权并不改变度与集聚程度等局域几何量，所以无权网络的局域几何量分析都可以在加权网络上实现。权的分布反映的是本领域内学术交流的活性，如果我们认为所有学术研究都将表现为文献发表与学术交流的话，那么它反映的是此领域内学术研究的活跃程度。

类似于无向网络的度相关性，权的相关性考察的内容是是否活跃的科学家倾向于和其他活跃的科学家合作，还是倾向于提携后进。一种可行的方法是把某一个点的权定义为从该点出发的所有的边的权重之和，即

W^out_u = $\displaystyle \sum_{{v\in V}}^{}$ W^out_uv $\displaystyle \delta^{{uv}}_{}$

(8)

Wⁱⁿ_u = $\displaystyle \sum_{{v\in V}}^{}$ Wⁱⁿ_vu $\displaystyle \delta^{{vu}}_{}$

(9)

权与度的相关性研究，考察的是科学家合作交流的广泛性与深入性的关系。用上一小节有向网络的度的定义，每一格点的有两个度值 d^out_u, dⁱⁿ_u，两个权值 W^out_u, Wⁱⁿ_u，存在四种相关性-- W^outd^out, W^outdⁱⁿ, Wⁱⁿd^out, Wⁱⁿdⁱⁿ。忽略有向性，可以定义

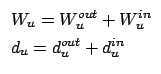
$\displaystyle \left\{\vphantom{ \begin{array}{l} W_{u}=W^{out}_{u}+W^{in}_{u} \\ d_{u}=d^{out}_{u}+d^{in}_{u} \end{array} }\right.$ $\displaystyle \begin{array}{l} W_{u}=W^{out}_{u}+W^{in}_{u} \\ d_{u}=d^{out}_{u}+d^{in}_{u} \end{array}$

(10)

在无权网络中，我们的研究关注于网络的联接结构与几何性质的关系；在加权网络中，研究的中心问题应该是权的加入对网络几何性质的影响，以及权与联接之间的关系，也就是权的几何性。例如我们可以通过打乱实际加权网络权与边的匹配方式来考察网络性质的改变。当然，在加权网络中，可能需要定义更好地反映其特征的几何量，例如在文献[12]中所提出的全局与局域效率的概念。但是文章提出的效率的概念还不足以突出权的影响。我们可以提出新的网络效率的概念，并讨论它与权的关系。作为一个初步的理论模型，我们可以在无权网络的基础上按照一定的方式给联接加上权重从而形成加权网络。一个可能的方法是，按照边的介数来赋权，考察这种付权方式对网络效率的影响，然后保持权重集合不变的情况下打乱权与介数的匹配，再考察这种打乱后网络效率的变化。利用这种方法就可以弥补缺乏加权网络模型导致的不方便。当然，从另一方面，也可以在实际加权网络上进行同样的讨论。这样的研究不仅能够探讨权的几何性，还能够启发加权网络模型的研究。

U_v = $\displaystyle {\frac{{W_v}}{{d_v}}}$ ,

(11)

加权网络中的最短路径是指在两点之间所有连通的路径中，权数之和最小的一条或几条路径。在科学家网络中，它和新的思想在网络上的传播密切相关。与无权网络的顶点数最小相比，加权会改变最短路径。而且由于最短路径的改变，介数也将发生变化。在科学家网络中，介数反映了在本领域内，某位科学家影响力的大小。某一顶点的近邻顶点介数分布的两极分化性质称为隧道现象[66]，全部顶点的介数分布反映的是科学家影响力的层次。边的介数反映的是不同科学家之间的交流对学科发展的影响力的不同。同时，利用边的介数也可以对科学家做类聚分析。所有以上局域或全局几何量都需要与相应的无向网络或无权网络做对比研究。

最后，我们可以用两两顶点之间的距离来度量由于加权带来的顶点之间的亲密程度的不同。并且有了距离关系以后，我们就可以做类聚分析，给出科学家之间的交流集团。这种类聚分析还可以和基于边的介数的类聚分析对比。加权网络目前仍然是一块有待开发的沃土。