Small World网络

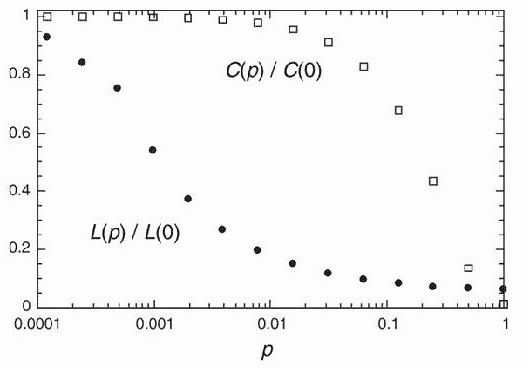
Watt和Strogatz发现，只需要在规则网络上稍作随机改动就可以同时具备以上两个性质。改动的方法是，对于规则网络的每一个顶点的所有 边，以概率p断开一个端点，并重新连接，连接的新的端点从网络中的其他顶点里随机选择，如果所选的顶点已经与此顶点相连，则再随机 选择别的顶点来重连。当p = 0时就是规则网络，p = 1则为随机网络，对于0 < p < 1的情况，存在一个很大的p的区域，同时拥有较大的集聚 程度和较小的最小距离。Small World网络的生成方法见图(1)，其中左图为规则网络，右图为随机网络，中间是一个典型的Small World 网络。Small World网络的几何性质如图(2)所示。

Fig 2: Small World网络的几何性质 同时有大集聚程度而小最短距离是Small World网络的重要特征，而且 此性质在p略大于0到小于1的很大范围内存在。本图取自文献[7]。

实证研究发现，大量的实际网络存在这种Small World现象，见表1。在Watts和Strogatz的工作之后，不同的作者做了许多Small World 网络上的动力学模型的研究[15,37,38,39,60,61,62,63]，体现了平均集聚程度和平均最短距离的 深刻的表现能力。我们将在网络的动力学性质一节对此做一小结。

4表1：实际网络的Small World现象。列表中包括所研究网络的实际对象（Network），大小（Size）， 平均度值（< k >），平均最短距离（l），按随机网络计算的最短距离（l_rand），平均集聚程度（C）， 按随机网络计算的集聚程度（C_rand）。通过对比实际网络与相应（相同顶点数和边数）随机网络的性质， 可以发现网络的Small World特征。此表在文献[1]的基础上收集确认其他文献编辑而成，感谢作者 R. Albert提供。

Network	Size	$\left\langle\vphantom{ k}\right.$k$\left.\vphantom{ k}\right\rangle$	l	lrand	C	Crand
WWW[31], site level, undir.	153, 127	35.21	3.1	3.35	0.1078	.00023
Internet[22] , domain level	3015 - 6209	3.52 - 4.11	3.7 - 3.76	6.36 - 6.18	0.18 - 0.3	0.001
Movie actors[7]	225, 226	61	3.65	2.99	0.79	0.00027
LANL co-authorship[66]	52, 909	9.7	5.9	4.79	0.43	1.8 x 10-4
MEDLINE co-authorship[66]	1, 520, 251	18.1	4.6	4.91	0.066	.1 x 10-5
SPIRES co-authorship[66]	56, 627	173	4.0	2.12	0.726	0.003
NCSTRL co-authorship[66]	11, 994	3.59	9.7	7.34	0.496	x 10-4
Math. co-authorship[67]	70, 975	3.9	9.5	8.2	0.59	5.4 x 10-5
Neurosci. co-authorship[67]	209, 293	11.5	6	5.01	0.76	.5 x 10-5
E. coli[52] , substrate graph	282	7.35	2.9	3.04	0.32	0.026
E. coli[52], reaction graph	315	28.3	2.62	1.98	0.59	0.09
Words[49], co-occurrence	460, 902	70.13	2.67	3.03	0.437	.0001
Power grid[7]	4, 941	2.67	18.7	12.4	0.08	0.005
C. Elegans[7]	282	14	2.65	2.25	0.28	0.05