

Next: 结束语
Up: 解析与数值计算方法
Previous: 随机网络的几何性质
对偏好依附模型的一般处理方法包含连续性方法[18,21],速率方程[20,23],Master方程[19]与
生成函数方法[9],这也是统计物理学经常使用的方法。这一节,我们围绕偏好依附模型的幂率分布形式介绍连续性方法,
速率方程与Master方程在复杂网络研究中的应用。
考虑Scale Free网络的偏好依附模型,从顶点的度值变化的角度,假设其度值连续,我们有如下方程,
每一步我们加入m条边,即增加2m个度值,于是
 kj = 2mt + m0,则
kj = 2mt + m0,则
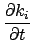 = = 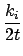
|
(29) |
顶点ki是在ti时刻进入系统的,且满足初始条件
ki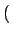 ti
ti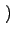 = m,于是
利用上式,结合ti的分布,就可以知道任意t时刻ki的分布,即
在t时刻,
ti
= m,于是
利用上式,结合ti的分布,就可以知道任意t时刻ki的分布,即
在t时刻,
ti 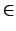
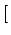 0, t
0, t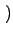 的分布函数为
的分布函数为
P(ti) =  . .
|
(32) |
结合以上两式就可以得到ki的分布,
P(k) = 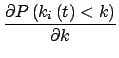 = = 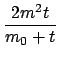 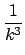  2m2k-3(t 2m2k-3(t 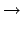 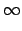 ). ).
|
(33) |
方程(28)是一种平均意义上的描述,实际随机过程中所加入的边只是按照
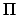
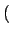 ki
ki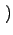 的分布来选择,并不能保
证确实让每一个顶点的度值增加那么大,也正是因此称为连续性方法,所以对实际随机过程分布函数演化的描述需要用到其他方法。引入分布
函数
p
的分布来选择,并不能保
证确实让每一个顶点的度值增加那么大,也正是因此称为连续性方法,所以对实际随机过程分布函数演化的描述需要用到其他方法。引入分布
函数
p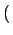 k;ti, t
k;ti, t ,表示ti时刻引入系统的顶点在t时刻度值为k的几率,其初始条件为
p
,表示ti时刻引入系统的顶点在t时刻度值为k的几率,其初始条件为
p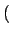 k;ti, ti
k;ti, ti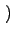 =
= 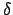
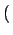 k - m
k - m ,,满足如下Master方程,
,,满足如下Master方程,
p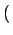 k;ti, t + 1 k;ti, t + 1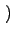 = p = p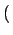 k;ti, t k;ti, t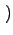 + wget + wget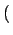 k - 1 k - 1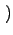 p p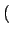 k - 1;ti, t k - 1;ti, t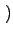 - wget - wget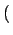 k - 1 k - 1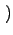 p p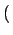 k;ti, t k;ti, t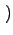
|
(34) |
其中
wget k
k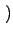 =
= 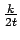 。所有顶点的度值分布定义所有不同时刻加入系统的顶点的平均行为,即
有以上两式可以求得度分布
。所有顶点的度值分布定义所有不同时刻加入系统的顶点的平均行为,即
有以上两式可以求得度分布
速率方程从另一个分布空间描述。t时刻度值为k的顶点组成一个集团,集团大小为
Nk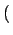 t
t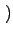 。当新顶点进入系统时,
Nk可能发生改变,其变化率满足如下方程,
。当新顶点进入系统时,
Nk可能发生改变,其变化率满足如下方程,
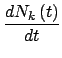 = mWget = mWget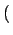 k - 1 k - 1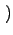 - mWget - mWget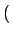 k k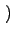 + + 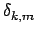 . .
|
(37) |
其中
Wget k
k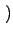 为所有度值为k的顶点获得新的联接的几率,
Nk同样满足方程
为所有度值为k的顶点获得新的联接的几率,
Nk同样满足方程
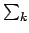 kNk
kNk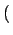 t
t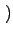 = 2mt + m0,且
结合一上方程可以解得度分布
P
= 2mt + m0,且
结合一上方程可以解得度分布
P k
k ,具体计算见文章[20,23]。
,具体计算见文章[20,23]。


Next: 结束语
Up: 解析与数值计算方法
Previous: 随机网络的几何性质
wwwwjs
2004-01-04
 .
.
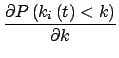 =
= 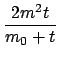
![]()
![]() ki
ki![]() 的分布来选择,并不能保
证确实让每一个顶点的度值增加那么大,也正是因此称为连续性方法,所以对实际随机过程分布函数演化的描述需要用到其他方法。引入分布
函数
p
的分布来选择,并不能保
证确实让每一个顶点的度值增加那么大,也正是因此称为连续性方法,所以对实际随机过程分布函数演化的描述需要用到其他方法。引入分布
函数
p![]() k;ti, t
k;ti, t![]() ,表示ti时刻引入系统的顶点在t时刻度值为k的几率,其初始条件为
p
,表示ti时刻引入系统的顶点在t时刻度值为k的几率,其初始条件为
p![]() k;ti, ti
k;ti, ti![]() =
= ![]()
![]() k - m
k - m![]() ,,满足如下Master方程,
,,满足如下Master方程,
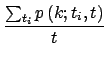 .
.
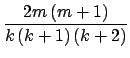
![]() t
t![]() 。当新顶点进入系统时,
Nk可能发生改变,其变化率满足如下方程,
。当新顶点进入系统时,
Nk可能发生改变,其变化率满足如下方程,
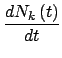 = mWget
= mWget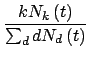 .
.
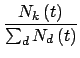 .
.