随机网络的几何性质

图论与概率论是网络研究的重要工具。在随机网络模型一节，我们已经了解，包含n个顶点的随机网络有两种 G$\left(\vphantom{n,M}\right.$n, M$\left.\vphantom{n,M}\right)$ 与 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$。现在我们用这两种网络分别构造两个概率空间。记 N = C²_n， G$\left(\vphantom{n,M}\right.$n, M$\left.\vphantom{n,M}\right)$包含了C^M_N 个可能的网络，假设所有的网络等几率，则 G$\left(\vphantom{n,M}\right.$n, M$\left.\vphantom{n,M}\right)$成为概率空间。给定网络 H $\in$ G$\left(\vphantom{n,M}\right.$n, M$\left.\vphantom{n,M}\right)$的几率为

P(G_M = H) = (C^M_N)^-1. (23)

对于随机网络 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$，实际上它包含了2^N个所有可能的网络，从空图到完全图。记 e$\left(\vphantom{H}\right.$H$\left.\vphantom{H}\right)$为网络H的边数， 给定网络 H $\in$ G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$的几率为

$$\left(\vphantom{H}\right. \left.\vphantom{H}\right) \left(\vphantom{1-p}\right. \left.\vphantom{1-p}\right)^{{N-e\left(H\right)}}_{}$$ (24)

从统计物理学系综理论的角度我们可以这样来看概率空间 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$。我们把 e$\left(\vphantom{H}\right.$H$\left.\vphantom{H}\right)$看作图H的宏观量，类比于 物理系统微观状态的能量，概率空间 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$关于e的分布为

$$\left(\vphantom{1-p}\right. \left.\vphantom{1-p}\right)^{{N-e}}_{}$$ (25)

而边为e的微观图也构成概率空间 G$\left(\vphantom{n,e}\right.$n, e$\left.\vphantom{n,e}\right)$，其中每一个图都等几率。所以随机图 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$是正则系综， G$\left(\vphantom{n,e}\right.$n, e$\left.\vphantom{n,e}\right)$则可以认为是微正则系综。

在组合系数C^e_N上，图论与统计物理学有不同的处理方式。图论定义了图的同态关系--如果图 V$\left(\vphantom{G_{1}}\right.$G₁$\left.\vphantom{G_{1}}\right)$与 V$\left(\vphantom{G_{2}}\right.$G₂$\left.\vphantom{G_{2}}\right)$ 之间存在可逆映射 $\phi$ : V$\left(\vphantom{G_{1}}\right.$G₁$\left.\vphantom{G_{1}}\right)$ $\rightarrow$ V$\left(\vphantom{G_{2}}\right.$G₂$\left.\vphantom{G_{2}}\right)$，使得对于 $\forall$x, y $\in$ V$\left(\vphantom{G_{1}}\right.$G₁$\left.\vphantom{G_{1}}\right)$， 如果 xy $\in$ E$\left(\vphantom{G_{1}}\right.$G₁$\left.\vphantom{G_{1}}\right)$则 $\phi$$\left(\vphantom{x}\right.$x$\left.\vphantom{x}\right)$$\phi$$\left(\vphantom{y}\right.$y$\left.\vphantom{y}\right)$ $\in$ E$\left(\vphantom{G_{2}}\right.$G₂$\left.\vphantom{G_{2}}\right)$。所以给定图H相当于给定了H 以及与H同态的所有图。从统计物理学来看，这相当于顶点不可区分的情况，这时候网络结构成为不同网络的唯一区别，同态图就如同微观 状态的简并度。但是对于顶点可区分的网络，在网络结构相同的情况下，相同的连结方式连在不同顶点上仍然有值得区分的意义。由于目前 研究的实际系统顶点都是可以区分的，我们不考虑网络的同态。

当我们说随机图 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$具有性质Q指的是在随机图的概率空间中，从平均意义上有性质Q。现在我们讨论随机网络 顶点的度值分布。我们首先对于每一个微观图统计其顶点度值分布规律，然后按照不同微观图出现的几率做一个平均，就可以解决这个问题。 但是，即使对于微正则系综 G$\left(\vphantom{n,e}\right.$n, e$\left.\vphantom{n,e}\right)$中的样本点也存在不同的度值分布形式，因而实际上实现这一方法并不简单。现在我们换一个近似的 方法。由正则系综分布函数(25)式可见，分布函数的最大值点是边数的平均值 $\bar{{e}}$ = Np，且二项分布衰减的非常快，因此，我们 可以尝试在分布函数峰值附近的微观图上最近似的平均。这样，问题就变成微正则系综随机图 G$\left(\vphantom{n,Np}\right.$n, Np$\left.\vphantom{n,Np}\right)$的度值分布形式。

重新表述问题如下：在n个顶点的网络中等几率地选取 ${\frac{{1}}{{2}}}$n(n - 1)p条边，求平均意义上顶点被选取次数的分布形式。首先，我们来看某 一个顶点被选取的几率$\rho$。在第一条边的选取的时候，每一个顶点具有(n - 1)条可以被选取的边，被选取的几率相同，又因为每选取 一条边产生两个顶点，所以任一顶点被选取的几率 $\rho$ = ${\frac{{2}}{{n}}}$。假设p $\ll$ 1，则被选取的边并不影响与其关联的顶点再次被选 取的几率。因此几率为$\rho$的顶点被选取的近独立事件构成概率空间，其分布符合平均值为 $\lambda$ = $\rho$ x ${\frac{{1}}{{2}}}$n(n - 1)p = (n - 1)p $\doteq$ np 的泊松分布，即

$${\frac{{\left(pn\right)^{k}}}{{k!}}}$$ (26)

一个更有物理学风格的方法[1]是计算在随机图 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$中，一个顶点可能有的所有联接数，尽管此联接数不一定是某个网络中它的度值 的含义，

P(k_i = k) = C^k_n-1p^k(1 - p)^n-1-k. (27)

对所有的k_i作频数统计，当n很大时，上述二项分布可以用(26)式泊松分布代替。

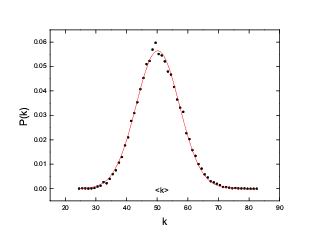
当然，解决度分布问题更加直截了当的方式是产生足够多的随机图样本点，然后进行统计。按照二项分布的尖峰特征，只要少量的样本就可以 得到比较准确的网络性质。见图(5)，图中只用了一个微观图来计算。当我们实际拿到一个网络的数据进行分析时，一般我们直接 在这个网络上统计性质Q是否存在，很少需要大量的同质网络组成系综来讨论。这与统计物理中实际测量一个系统是一样的。我们的理论是 建立在宏观状态与微观状态的关系的基础上的，但是对于实际测量，我们也只需要一个系统就可以了。

Fig 5: 随机网络的度分布：图上各点来自于随机生成的一个随机网络，其中N=20000，p=0.0025；连线 为用于拟合的泊松分布。

随机网络研究的另一个重要方面是与统计物理学联系在一起的相变现象，这也是随机网络得到充分研究的原因之一。随机网络的相变现象表现 为几何性质随着参数p的突现性，存在很多的几何性质Q只有当 p > p^Q_c才会出现，展现出类似于二级相变的行为。例如我们讨论网络 最大集团的相对大小。图的一个连通子图称为图的集团，其中顶点数最多的称为最大集团。所研究的问题是p值对网络最大集团相对于整 个网络的相对大小的影响。记最大集团大小为S，其相对大小为 s = ${\frac{{S}}{{n}}}$。可以看到，如果 p $\approx$ 1则，最大集团与整个网络 大小相当，而 p $\approx$ 0则相反。那么，0 < p < 1的情况呢？这在随机网络的研究中被称为网络的演化性质。

研究这些问题要用到随机图演化序列构成的概率空间 $\tilde{{G}}^{{n}}_{}$，定义为从空图到完全图的随机图序列 $\tilde{{G}}$ : = G$\left(\vphantom{n,0}\right.$n, 0$\left.\vphantom{n,0}\right)$, G$\left(\vphantom{n,1}\right.$n, 1$\left.\vphantom{n,1}\right)$,..., G$\left(\vphantom{n,N}\right.$n, N$\left.\vphantom{n,N}\right)$组成的等几率空间，其中 G$\left(\vphantom{n,t}\right.$n, t$\left.\vphantom{n,t}\right)$表示t时 刻的图，也表示有t条边的图。当 n $\rightarrow$ $\infty$时这个空间可以看成是由各个 G$\left(\vphantom{n,M}\right.$n, M$\left.\vphantom{n,M}\right)$空间中组合而成，或者看成由不 同p值的 G$\left(\vphantom{n,p}\right.$n, p$\left.\vphantom{n,p}\right)$空间组合而成的空间。关于s的问题就可以在这样的概率空间中得到研究。结果表明对于最大集团， 当 p < p^s_c = ${\frac{{1}}{{n}}}$时不存在大规模集团，当 p = p^s_c = ${\frac{{1}}{{n}}}$时，最大集团大小为 S $\sim$ n^{${\frac{{2}}{{3}}}$}，当 p > p^s_c = ${\frac{{1}}{{n}}}$时最大集团大小S $\sim$ n。

熟悉统计物理渗流理论的话就会很容易发现这种现象与渗流理论的联系。实际上他们本来就是同一件事情，只不过从不同的角度进行研究。例 如我们知道，在渗流问题中，在p = p_c附近，各连通集团的规模展现幂率分布。同样，在随机网络中，也存在这种幂律形式的规模分布。