l-1 = 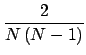 |
(19) |
从Small World网络模型可以发现,之所以它具有独特的几何性质,并由此带来Samll World网络上动力学模型的特殊性质,完全是因为加入 了极少量的长程联接的缘故。因此,对于Small World网络,只要能够识别这些长程联接,然后针对长程联接进行攻击就可以在很大程度上 改变Small World网络的结构。所以对于Small World网络的攻击的关键问题是长程联接的识别。这并不是一个平庸的问题。对于规则网络 的基础上改造而得的Small World网络,直观上我们就能够识别长程联接。但是如果把点的顺序打乱重新再做一次图,那长程联接与短程联 接就不好区分了。恰恰当我们面对实际网络的时候,这种关于顶点的先验顺序实际上就是不存在的。Pandit和Amritkar[40]最 先研究了这一问题,提出了一种基于各阶路径的边的阶数的定义,然后由边的阶数来反映其长程还是短程联接。但是这种识别方法不具有 很好的区分能力。有一个很好的几何量--边的介数--可以很好地区别长程与短程边。边的介数的含义是所有最短路径中必须经 过此边的次数。长程联接一般联接着两个局域集团,因此不同的集团的两点之间的最短路径就会经过这条长程联接。而不同集团之间的顶 点对的数目 C2n1+n2远远大于集团内部顶点对数目之和 C2n1 + C2n2,其中 n1, n2为两集团顶点数。 因此可以把边的介数做为判断长程联接的一种方法。Motter等人的文章[41]就研究了基于边的介数的攻击方式,发现Small World 网络对于这样的攻击方式非常敏感。对于Small World网络,可以预见,所谓结构发生很大改变就是平均最短距离变长了,平均集聚程度变小了。 因此,网络结构稳定性的研究,一般地从以下四个方面随着攻击的变化来讨论:平均最短距离,平均集聚程度,最大集团的相对大小以 及集团规模分布模式。有的文章还用特征路径长度代替平均最短距离来讨论,因为平均最短距离随着攻击幅度的增加而增加,与效率的通常 意义相反。特征路径长度的定义如下,
l-1 = 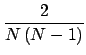 |
(19) |
对一般网络的攻击方式可以选择去点与去边两种方式,从选择的方式上分为随机攻击和选择性攻击两种类型[42],分别称为 网络的容错能力与抗攻击能力。研究表明[42,43],Scale Free 网络具有很强的容错性,但是对于基于顶点的度值或介数的选择性攻击抗攻击能力较差,对于基于边的介数的攻击也非常敏感。那么, 这些选择性攻击之间是否等价,有关联吗?如果按照顶点的度值所去掉的点与按照顶点的介数所去掉的点之间存在很强的共性的话, 我们就说其实这两种攻击等价。还可以进一步研究基于边的介数的去边攻击与前述去点攻击之间的关联性。当我们考虑这几个 关联性的时候,其实,已经从网络的结构稳定性回到了网络的静态几何性质。我们可以按照度值对所有顶点排序,然后我们可以再按照 顶点的介数排序,如果两个序列之间存在很强的关联性则认为两种方式等价。可见,网络的结构稳定性与网络的静态几何性质也是紧密 联系在一起的。文章[43]不仅讨论了网络的最短距离等几何性质在去边去点攻击下的改变,还讨论了度值与介数等几何量的 相关性。
实际网络的结构稳定性分析的一个重要实例是食物链网络。网络结构稳定性的理论研究表明,对于规则网络与随机网络等同质网络(每 个顶点都相同),随机攻击与选择性攻击的效果相当,Small World网络对于长程联接攻击非常敏感,Scale Free网络对于随机攻击具有 很强的鲁棒性,但是基于度值或介数的选择性攻击可以造成很大的结构性破坏。那么对于食物链网络呢?由于规模限制,食物链网络的度 分布没有得到最终的研究结果,存在幂率分布、均匀分布、以及指数分布等多种形式。在这样的网络上,如果发生个别物种的衰落或死亡 会对整体生态系统产生什么影响呢?Dunne等人的文章[57]对这个问题进行了研究。文章讨论了16个不同的食物链网络对随机 攻击和基于度值的选择性攻击的响应。定义引起50%以上物种灭绝的去点率做为网络鲁棒性的度量。发现尽管网络的结构有所不同,但 是网络的鲁棒性与网络联接的紧密程度具有很强的正向关联。但是这样的网络是否比同样顶点与边数的随机网络或Scale Free网络具有更 强的鲁棒性呢?还有,食物链网络是有向网络,以度值为基础的攻击方法不足以反映有向网络的特征,是否可以试一试基于顶点介数的攻 击方式呢?
网络结构稳定性问题另一个有意义的实例是SARS传染病的控制。我们认为SARS传染病是在居民基本活动网络上传播的疾病。近距离接触传 染是其主要传播方式。因此我们提出了以楼为顶点,人员流动为联接的居民基本活动网络。例如我的办公楼与家庭住所是网络中的两个顶点, 因为我的存在,这两个顶点之间建立了联接。这样一个网络应该包含居民的工作或学习、必需品与必要服务的获得等几个方面。有了这 样一个网络,加上关于传染病传播的更详细的调查,我们就可以以网络攻击为基础来讨论对传染病的控制。
首先,我们需要研究网络的基本结构特征,比如平均最短距离与平均集聚程度的特征,度分布等静态几何性质。然后,针对网络的特点 与传染病传播的特点制订预先切断某些联机接的方案,隔离某些顶点,改变网络性质。我们认为,传染 病的隔离控制包含两个方面,第一是对得病人员及其接触者的隔离,第二是对网络结构的预先隔离,也就是对健康人的工作、学习、生 活进行调整,例如在发现病人之前就有重点地隔离某些区域,限定某些人在家办公等等。由于条件所限,目前我们没有开展关于这个网 络的数据调查工作。Scale Free网络的攻击与网络上传染病的控制相结合的模型研究正在进行中,我们的目标是找到Scale Free网络上 的一种攻击方法,使得大规模迅速传播的传染病转为小规模缓慢传播。
鉴于目前SARS在全世界范围,尤其在中国部分省市的流行,研究这样一个问题就更加有紧迫性和实际意义了。实际网络研究还发现, 人类朋友关系网络[7],人类性伙伴网络[47]正是一个有Small World特征的Scale Free网络。在这样的网络上采用什么方 式来攻击,才能使传染病的流行得到控制,目前还有一个有待研究的问题[64]。
以上关于用隔离网络的方法控制传染病的讨论没有涉及隔离的代价问题。其实,在决策过程中,这是需要重点考虑的问题。例如从网络结构 的角度发现某一个重要顶点需要隔离,可是从经济以及社会效益的角度可能会发现隔离这个顶点的代价非常大,这时候就需要在两者之间取 得平衡。因此,我们需要在控制问题中就把代价包含在问题考虑之内。对于一般的网络攻击,代价也具有值得讨论的普遍意义。我们定义代 价正比于顶点或边的重要程度,即
|
(20) |
网络的效率是网络结构与功能关系的另一个重要组成部分。河流与血管的分支网络做为水流与血液的传输网络,其网络结构与传输效率
的关系在分形几何的研究中已经得到了深入的研究[59],发现了普适的分支行为标度律(Allometric Scaling)。
文章[59]还从理论上证明了,镶嵌在d维空间的树形传输网络,其最优效率下的分支系数为
![]() =
= ![]() 。
食物链网络可以认为是能量与物质流的传输网络,Garlaschelli等人[58]研究了这一网
络的结构与效率关系。首先从食物链网络中以环境为根节点产生一个最小生成树。对于树中的每一个顶点,定义包括直接与间接的上级顶点
数,即直接与间接捕食者数量Ai,定义顶点的耗散量
Ci =
。
食物链网络可以认为是能量与物质流的传输网络,Garlaschelli等人[58]研究了这一网
络的结构与效率关系。首先从食物链网络中以环境为根节点产生一个最小生成树。对于树中的每一个顶点,定义包括直接与间接的上级顶点
数,即直接与间接捕食者数量Ai,定义顶点的耗散量
Ci = ![]() Ak,其中k > i的含义是物种i的上级顶点。研究Ci
与Ai的关系发现,两者成幂律关系
Ak,其中k > i的含义是物种i的上级顶点。研究Ci
与Ai的关系发现,两者成幂律关系
|
C |
(21) |
网络结构与功能关系的另一个重要方面是利用网络独特的表现力发掘那些只能通过网络这个工具加以研究的对象。网络上交流集团的类 聚分析就是其中之一。网络上的顶点之间是存在某些交流集团的。例如WWW网络中,存在某一个领域内的网页相互联合的现象,科学 家网络中存在团队现象。这些联合或团队内部顶点之间的联接会比团队之间的联接更加频繁。那么,只要这样的几何结构存在,我们就 可以通过结构上的分析来发现这些团队,而不需要依靠内容。关于团队所对应的几何结构有两种方式来描述。第一,团队内部成员之间的 集聚程度会比团队之间的高。第二,不同团队的顶点之间的最短路径一般需要经过长程联接。联接赋权的等级类聚方法[6] (Hierarchical Clustering)基于第一种描述,而Newman[73]等人提出的基于边的介数的类聚方法的前提是第二种描述。 联接赋权方法的基本思想是,找到任意两个顶点之间的所有路径,包括最短路径,以及比最短路径长的其他路径,有时候可以只取到比 最短路径长3个顶点以内的路径,记下长度为l路径的条数nl。对于属于同一个集团内的两个顶点,存在各阶路径的条数显然要比不同集团的两个顶 点之间要多。因此定义亲密程度
|
S = |
(22) |