|
dv = |
(1) |
Ŀǰ�ѵõ��о��ĵ����������������Internet���磬��Ӱ��Ա�������磬��ѧ�Һ������磬�����Թ�ϵ���磬�����ʻ��������磬 ����ѧ���磬�������۵���ϵ���硣
��������Ļ���������[1,2]�У��ȼ���ֲ��������ȵ�����ԣ����۳̶ȼ���ֲ���������̾��뼰��ֲ�������������Betweenness�� ����ֲ���������ͨ���ŵĹ�ģ�ֲ���
һ������Ķ���ָ��˶������ӵıߵ���������
|
dv = |
(1) |
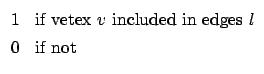 ; ;
|
(2) |
![]() v
v ![]() V���Ƕ����Եõ����dv����ֵ�ķֲ��������������Ҫ�������ʡ���������������ֵ��ͬ���������
V���Ƕ����Եõ����dv����ֵ�ķֲ��������������Ҫ�������ʡ���������������ֵ��ͬ���������![]() �ֲ���
���������ϲ��ɷֲ�����3.1�ڣ�������ʵ���������������ʽ�Ķȷֲ�[1,2]����Ϊ�ޱ��
���磨Scale Free Networks��������Internet����[44,45]����Ӱ����Ӿ���Ա��������[18,32,46]����ѧ�Һ�������[66,67]��
�����Թ�ϵ����[47]�������ʻ���������[48]������ѧ����[49]�ȣ�ͬʱ�����ڸ�˹
�ͣ��絰�����۵�����[46]����ָ��˥���͵ĸ��ʷֲ�������Ӿ���Ա��������[46]��
�ֲ���
���������ϲ��ɷֲ�����3.1�ڣ�������ʵ���������������ʽ�Ķȷֲ�[1,2]����Ϊ�ޱ��
���磨Scale Free Networks��������Internet����[44,45]����Ӱ����Ӿ���Ա��������[18,32,46]����ѧ�Һ�������[66,67]��
�����Թ�ϵ����[47]�������ʻ���������[48]������ѧ����[49]�ȣ�ͬʱ�����ڸ�˹
�ͣ��絰�����۵�����[46]����ָ��˥���͵ĸ��ʷֲ�������Ӿ���Ա��������[46]��
��һ���������ǣ��Ƿ�ȷֲ������걸����������������أ�����ȷֲ�������һһ��Ӧ�����Ǿ�˵�ȷֲ������������������磬����Ҳֻ�� Ҫ�öȷֲ����������������һ�����Ķȷֲ���ͨ�����������ǿ��Ը���Ӧ�����ÿһ������һ����ֵ�����ֶ�ֵ������һ�����ӷ�ʽ���� ��һ�����硣�������һ�����Ӷ�Ӧ��������������һ������������Ϊʵ����Ϊͬһ���硣������Ȼ���ܱ�֤����������Ҳ��һ������ô�� ���ֶ�ֵ�����������ӣ��������֮��û������ԣ��Ƿ���Գ�Ϊ���������Ĵ����أ����Զȷֲ�֮������������һ����Ҫ�ļ������� Newman������Ϊ��ƥ��ģʽ��[16]����˼�ǿ����ֵ��ĵ������ںͶ�ֵ��ĵ����ӣ����������ںͶ�ֵС�ĵ����ӡ�����ķ����ǣ�ͨ������һ�� �߶������ҵ��������㣬�����õ�������ֵ������ͨ�����еı����Ǿ͵õ����������У��������������е�����Լ��ɡ��о�����ʵ�� �������һ���̶��ϵ�ƥ��ģʽ���е���������ƥ�䣬Ҳ�е����練��ƥ�䡣���ǣ��������������磬����һ������Ķȷ�������a���� ��һ������Ķȷ�������b������ģ���һ���������Է�����Ӱ�첢û�еõ��о���ʵ������ķ�����������ͬ��������ڲ�ͬ��ƥ�� ģʽ���������Ҳ�и���ء�
���۳̶ȵ����������缯�Ż��ij̶ȣ�������������һ��ļ��Ÿ��ԵĽ���֮���ж����ǹ�ͬ�Ľ��ڡ�һ�ֶ����Ƕ���ÿһ������v����
������ڼ���Nv����
n = ![]() Nv
Nv![]() ��Nv�д��ڵıߵ�����Ϊ
��Nv�д��ڵıߵ�����Ϊ
M = 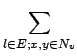 |
(3) |
|
Cv = |
(4) |
��������·��lij����Ϊ������ͨ
![]() i, j
i, j![]() ��ͨ·�У��������������������ٵ�һ������·������
��ͨ·�У��������������������ٵ�һ������·������
![]() i, j
i, j![]() ֮�����·���ļ���ΪSij����Ӧ��·������Ϊ
dij =
֮�����·���ļ���ΪSij����Ӧ��·������Ϊ
dij = ![]() lij
lij![]() �����
�����
![]() i, j
i, j![]() ֮�䲻����ͨ·����ô��dij = N���������ǿ��Եõ�
һ��N x N�ľ���
֮�䲻����ͨ·����ô��dij = N���������ǿ��Եõ�
һ��N x N�ľ���
![]() dij
dij![]() ����ֲ�������һ����Ҫ��ȫ�ּ���������ƽ��ֵ��Ϊƽ�����·��d��
����ֲ�������һ����Ҫ��ȫ�ּ���������ƽ��ֵ��Ϊƽ�����·��d��
��һ����Ҫ��ȫ�ּ������ǽ�����Betweenness��[17]������u�Ľ�������Ϊ���������е����·��֮�У�����u��������
����ӳ�˶���u��Ӱ��������
![]() i, j
i, j![]() ֮�����·���ļ���ΪSij������u�Ľ�������Ϊ
֮�����·���ļ���ΪSij������u�Ľ�������Ϊ
Bu = 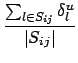 . .
|
(5) |
��ͨ������ָG��һ����ͼ���������ͼ�ڣ���������֮�䶼����ͨ·��һ��������ܴ��ڶ�����������ͨ���š�������ģ���У� ��ϵͳ�����ٽ�״̬ʱ����ͨ���ŵĹ�ģ���ֳ����ʷֲ���ʵ֤�о����������ڴ�����Scale-free ���磬��ͨ���ŵĹ�ģҲ�������ʷֲ�[1]��
������������Ķȷֲ�����������һ����ʽ��������ڶ������Ŀ�õ���ֵ��Ȼ������ж���Ķ�ֵ��һ�����ٰѽ��ڶ���Ķ�ֵ��ӵ� ������Ķ��ζ�ֵ���ظ� ��һ���̣�ֱ���õ��ȶ��Ķ�ֵ[6]�������õ���ÿһ������Ķ�ֵʵ�������ڽӾ���������ֵ��Ӧ�ı�����������������ʵ���Ͼ��Ǿ� ����ֵ�������½��������������Ķȷֲ����еļ�������Ŀǰû�еõ��о���