不同尺度下的生命系统充满着多样性和复杂性，同时又展现令人惊叹的共性。分别由大量细菌、蚂蚁、蝗虫、椋鸟、鱼、、绵羊等组成的生命系统，尽管它们的尺度和认知能力存在巨大的差异，但都可以涌现相似的集体运动。这些集体行为的背后存在什么普遍规律？生命系统从无序到集体运动的转变是一种相变吗？如果是，这种相变是连续的还是不连续？这些都是物理学家当前非常好奇和想回答的问题。

作为生命系统集体运动的一个简单模型，Vicsek模型[1]的粒子处于噪音环境下。噪声较强的时候，粒子随机运动、系统呈现无序。噪声较弱时，粒子运动方向趋向一致，涌现集体运动，Vicsek等人认为这是一种连续相变。但遭到后续研究的质疑[2]，认为他们看到的连续相变由有限尺度效应导致，实际应当是不连续相变。相变研究的关键量是序参量，集体运动涉及速度和密度，上述研究仅将平均速度作为序参量缺乏依据，也没获得有限尺度标度性的支持，结果不能作为定论。

最近发展的本征微观态方法[3]借鉴玻色-爱因斯坦凝聚的思想，通过统计系综本征微观态凝聚，确立系统的相变和对应序参量，已成功应用于伊辛模型、地球温度系统和股票市场等。将其用于Vicsek模型后发现：1）随着噪声减弱，首先发生密度相关本征微观态的凝聚，且为不连续相变；2）噪声进一步减弱，发生群体运动相关的本征微观态凝聚，为连续相变，不同Vicsek模型、不同系统密度的临界指数相同，属于同一个普适类。研究成果由学院陈晓松教授博士研究生李旭等合作完成，已作为亮点工作发表在Chin. Phys. B 2021, Vol. 30(12): 128703 DOI: 10.1088/1674-1056/ac3c3f.

此项工作回答了上面提出的问题，确立生命系统集体行为的转变是相变，而且存在着两类相变，分别是密度的不连续相变和群体运动的连续相变，不同连续相变属于相同的普适类。此外，这项展示了本征微观态方法对研究非平衡相变的可行性，为各类复杂系统非平衡相变的研究打开了一个通道。

[1] Vicsek T,  Czirok A, Ben-Jacob E, Cohenl I, and Shochet O 1995 Phys. Rev. Lett. 75, 1226.

[2] Gregoire G and Chate H 2004 Phys. Rev. Lett. 92, 025702.

[3] Sun Y, Hu G, Zhang Y, Lu B, Lu Z, Fan J, Li X, Deng Q, and Chen X 2021 Commun. Theor. Phys. 73, 065603.

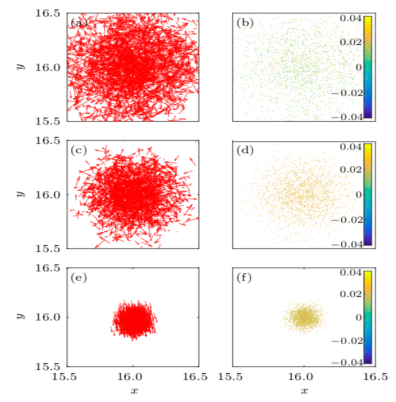
图1.  第一大本征微观态速度和近邻密度涨落空间分别。(a,b)对应噪声h="6" ，(c,d)对应噪声h="3.95，(e,f)对应噪声h="0.25.

作者：李旭，陈晓松

编辑：兰松

审核：王大辉