【成果】有向网络的双曲空间嵌入
文章“An Asymmetric Popularity-Similarity Optimization Method for Embedding Directed Networks into Hyperbolic Space”于2020年4月发表在SCI期刊《Complexity》。该文章的作者是吴宗柠(第一作者),狄增如教授,樊瑛教授(通讯作者)。
网络嵌入是当前网络科学中的热点话题,寻找复杂网络有效的低维空间表征有助于处理后续任务,如节点分类、链路预测、推荐算法等等。复杂网络理想的空间嵌入是双曲空间,将复杂网络几何化的同时又不损失复杂网络中无标度、小世界以及高集聚性等性质。已有的研究关注的是无向网络及其应用,然而绝大多数的实际网络都是有向的,忽略复杂网络的方向性极大地限制了复杂网络双曲几何模型的应用场景。
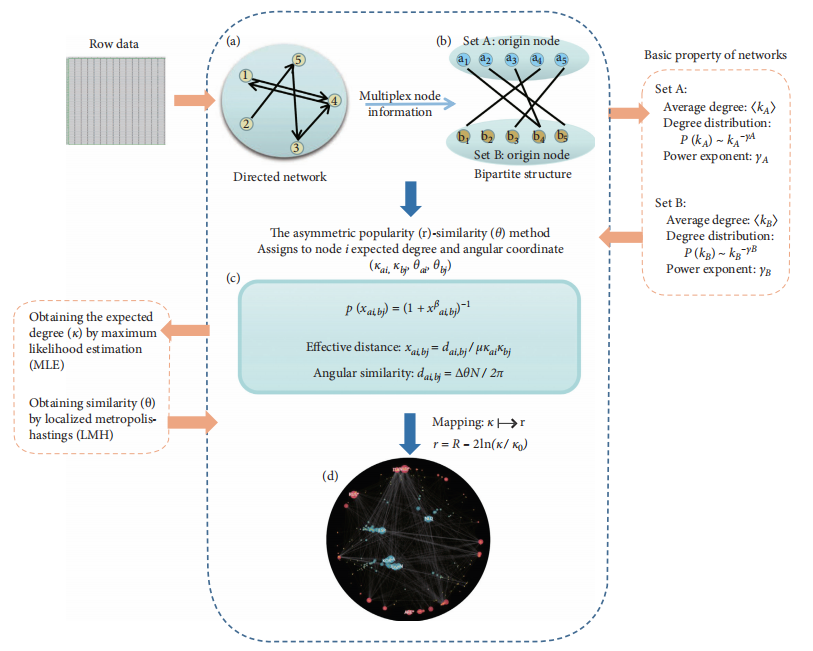
本文首次提出了适用于有向网络的双曲空间嵌入模型。该模型根据有向网络的二分结构和多路复用节点信息,展示了有向边在双曲空间中的连接模式。有向网络双曲嵌入的关键在节点双曲坐标的估计。为此,文章给出了非对称流行度-相似度优化(APSO)方法,即在已知有向网络的拓扑结构的条件下,通过极大似然估计推断出节点在双曲空间的位置。在双曲嵌入过程中,文章从AUC、理论模型与模拟结果对比,以及网络拓扑结构特征(度分布、集聚系数分布和介数中心性分布)等角度实证了该算法的有效性。此外,该方法还被用于国际贸易系统和C.elegance神经网络系统的研究。
北京师范大学系统科学学院狄增如教授和樊瑛教授的研究小组多年来一直从事复杂性科学、复杂网络等相关领域的研究,这是近年来关注复杂网络与网络表征学习等交叉领域所产生的研究成果。该研究得到了国家自然科学基金项目(71731002, 61573065)和北京师范大学博一学科交叉基金项目(BNUXKJC1921)的资助。
文章链接:https://www.hindawi.com/journals/complexity/2020/8372928/


