高维度和动态性是复杂系统的显著特征。如何在高维动态环境中实现高效的认知和决策是脑科学、人工智能和管理科学等领域共同面临的难题。针对这一难题，北京师范大学系统科学学院斯白露教授研究团队提出了一个多维二值波动环境下层次化贝叶斯在线推断与决策模型。这一成果于2022年12月以《A Hierarchi-cal Bayesian Model for Inferring and Decision Making in Multi-Dimensional Volatile Binary Environments》为题在SCI期刊《Mathematics》上在线发表。

这项工作以高维二值波动环境中的感知和决策为研究问题，基于贝叶斯理论建立多维二值波动环境下的层 次化贝叶斯在线推断与决策模型，包括层次化贝叶斯推断模型和贝叶斯(决策) 响应模型两个部分。针对多维二值波动环境下的感知问题，模型采用多维独立伯努利分布刻画环境的感知信息，基于团队前期提出的一般层次化布朗滤波(General Hierarchical Brownian Filter, GHBF)框架建立多维二值波动环境下的层次化贝叶斯在线推断模型，动态地刻画环境中多个维度之间的相关性，捕捉多维独立伯努利分布的自然参数随时间的变化和波动，多维独立伯努利分布相对一般多维伯努利分布(考虑各个维度之间的交互) 简单易用，但是丢失了各维度之间的交互属性， 无法捕捉和理解高维环境内在的结构特征。这 一工作通过GHBF框架引入了多维独立伯努利分布自然参数的低阶交互(皮尔逊相关性)，从而使模型可以高效地估计二值波动环境中存在的关联模式结构。在此基础上，这一工作基于变分贝叶斯推断框架，建立了一族具有预测编码能力的闭环模型更新方程，使模型能够根据环境的波动自适应地进行在线学习。

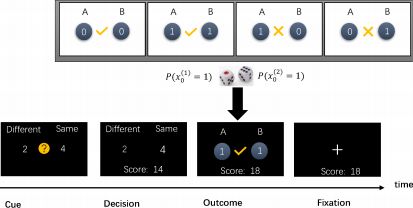
图 1:二维二值波动环境中的博弈任务：任务包含四个阶段。 (1) 线索提示(Cue)：两个选项及其选对时的分数奖励被呈现; (2) 决策(Decision)：一旦博弈者做出了选择, 所选择的选项将会以放大高亮方式呈现;(3) 输出结果(Outcome)：两个臂随机生成它们各自的状态, 同时输出博弈者决策的结果。如果博弈者的选择是正确的，当前得分奖励加入总分中； 如果博弈者选错则不得奖励分，其总分值保持不变。 (4) 注意(Fixation)：这是两个试次之间的短暂休息。屏幕仅呈现当前博弈者的得分数，直到下次试次开始。

进一步地， 团队基于贝叶斯决策理论构建了一个贝叶斯响应模型，根据一般层次化布朗滤波(GHBF) 编码的二值波动环境信息做出概率最优的决策。受认知神经科学中的抉择研究启发，团队以多臂赌博机(multi-armed bandits, MAB)为基础设计了博弈任务，展示了高维二值波动环境下层次化贝叶斯在线推断与决策模型的工作机制。MAB是认知神经科学、机器学习、经济学等领域中广泛讨论的抉择问题，用于研究在不确定环境中进行抉 择时探索与利用的平衡。在一个多臂赌博机任务中，每个臂被抽象成两个状态——0 和 1，即“无奖励”和“有奖励“。某一时刻，多个臂的状态构成了一个多维二值随机变量。一般地，每个臂状态为 1 的概率随时间在不断变化，那么这些臂就构成了一个多维二值波动环境。基于波动的多臂赌博机(MAB) 环境，团队构造了一个判断两个臂(Arm A和 B) 的状态是否相同的博弈任务(图 1)。在这一任务中，两个臂(Arm A和 B) 状态为1的概率是时变的(图 2)，而且两个臂的状态概率随时间表现出不同程度的相关性，用于模拟自然条件下复杂系统的动态性和不同维度之间的交互作用。在这一博弈任务中，如果两个臂的状态相同，正确的决策对应选项 “Same”；如果两个臂的状态不同，其对应选项为“Different”。这两个选项用二值动作变量a=1(Same) 和a=0(Different) 分别表示。

图2: 两个臂的期望状态。 a.Arm A的期望状态随时间的变化(黑线)。b. Arm B的期望状态随时间的变化(黑线)。

随着环境的波动，不同维度的状态随时间发生变化，模型仍然能很好地跟踪多维环境的状态(图3b,c)，而且能动态刻画维度之间的相关性(图3d)。模型依据环境状态表征和奖赏信息作出决策(图3a,e)，比强化学习中的经典决策模型具有更好的稳定性，而且性能接近理想决策行为的最优性能(图3f)。

这项研究为解决不确定动态环境中的感知和决策问题提供了一个通用理论模型，能进一步应用于解析大脑抉择过程的信息处理机制，还可以扩展用于预测高维复杂系统的演化，对刻画生物集群群体运动中的长程作用、高维非线性动力系统的内在结构等具有广泛的借鉴意义。这一工作由北京师范大学、北京脑科学与类脑研究中心、中国科学院沈阳自动化研究所联合完成，得到了科技部科技创新 2030-“脑科学与类脑研究“ 重大项目2022ZD0205000的支持，第一作者是博士生朱昌波。

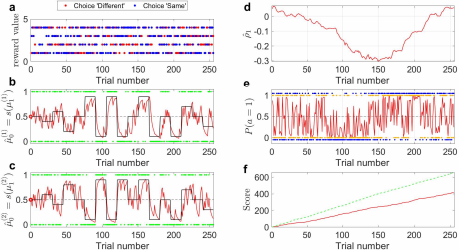
图 3:博弈任务中贝叶斯智能体后验状态的时间动态过程。 (a)博弈任务的奖赏分布。两个选项 “Different”和“Same”的奖励分数值随机地从离散均匀分布U(1, 4) 中采样。蓝点是每个试次中“Same”选项选对时的奖励分数值，红点是每个试次中 “Different” 选项选对的奖励分数值。(b),(c) 贝叶斯智能体对臂 A和 B的概率估计。绿点是感知输入(臂 A/B的状态)。红线表示臂A/B状态为1的后验概率估计。黑线是臂 A/B状态为1的真实概率。(d)模型捕捉到的自然参数的预测相关性。(e)贝叶斯智能体的决 策行为。橘黄色的点是模型在每个试次中做出的动作选择 a。蓝点是上帝视角下奖励最大时的理想动作 aideal(不一定是概率最优动作)。红线是两个臂 状态相同时的期望概率 (P (a =1)) 的轨迹。(f)模型的决策性能。绿色虚实线是采取理想动作时的累计最大奖励分数。红色线是模型实际累计奖励曲线，与理想条件下的最优性能保持相似的增长趋势。

作者：斯白露

审核：王大辉

编辑：郝林青